Suppose you have a linked list, now you have to identify whether there is any cycle in that linked list or not. This type of question is quite common for the interview. Today we will try to solve this problem using Floyd’s cycle finding algorithm.

In the picture above, a cycle with length $7$ is present in the linked list.
Detect Cycle In A Linked List
The easiest way to detect a cycle is to use a dictionary or hashmap. For that, we need to traverse the list from the very first node and save each node in the dictionary. After reaching to any node, if that node is found to be already present in the dictionary, then the linked list is cyclic. The complexity and memory complexity of this algorithm is $O(n)$.
But we can reduce the memory complexity of this algorithm to $O(1)$ using Floyd’s algorithm. It is also known as the ‘Hare and turtle’ algorithm.
Hare And Turtle Algorithm
Let’s assume we have two pointers; one is the turtle pointer, which we will denote by $’T’$, and the other pointer is the hare pointer, which we will denote by $’H’$. In the beginning, both of the pointers will be at the root node of the linked list.

In each second, the $H$ pointer will move two steps, but the $T$ pointer will move only one step. Then after one second, the position of the two pointers will be like this :
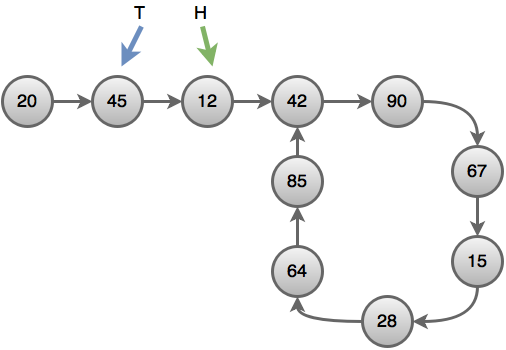
After one more additional second, $T$ will be at node $12$ and $H$ at the node $90$. After simulating these steps for some time, we will find that the two pointers will meet at the node $28$.

If the two pointers meet at the same node, it indicates that there is a cycle present in the linked list. If there were no cycles in that list, then the $H$ pointer would reach the endpoint of the list by approaching ahead.
Now the question is how we can detect the first node of the cycle?

How To Detect The First Node of The Cycle
Let’s assume,
$m$= distance between the root node and the first node of the cycle,
$k$= distance between the first node of the cycle and the meeting point of the two pointers.
$l$= length of the cycle.
Now, if $T$ meets $H$ after circling the cycle for $C_{T}$ times, then the distance traveled by $T$ will be:
$D_{T}=m+(C_{T}∗l)+k$
And, if $H$ meets $T$ after circling the cycle for $C_{H}$ times, then the distance traveled by $H$ will be:
$D_{H}=m+(C_{H}∗l)+k$
As the $H$’s speed is two times of $T$’s speed, so we can say that:
$2∗(m+(C_{T}∗l)+k)=m+(C_{H}∗l)+k$
After some rearranging, it can be written as:
$m+k=(C_{H}–2∗C_{T})∗l$
Here, $l$ is the length of the cycle, so $m+k$ is a multiple of the length of the cycle. It means that if we travel $m+k$ length from the first node of the cycle, then we will return to the first node again. This is the most important part of the algorithm to understand.
Now, if you move $m$ steps ahead from the meeting point, then you will return to the first node of the cycle again. The cause is, the distance from the first node of the cycle to the meeting point is $k$. But, the value of both $m$ and $k$ is unknown. Then, how can you move $m$ steps?
The Value of $m$
An interesting and quite easy way is there to determine the value of $m$. I hope you still remember that the distance between the root node and the first node of the cycle is also $m$.
Let’s assume; no $H$ pointer is there anymore, but another turtle pointer $’T_{2}’$ is now present at the root node, and $T$ is still in that meeting point. Now, if you move both the $T$ and $T_{2}$ pointer one step at a time, then the point where these two pointers will meet is the first node of the cycle!
This is the cycle detection algorithm of Floyd. The time complexity of this algorithm is still $O(n)$ (Why?), but the memory complexity has reduced to $O(1)$.
C++ Code for Cycle Detection Algorithm
Let’s see a $C++$ code here:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 |
/** * Definition for singly-linked list. * struct ListNode { * int val; * ListNode *next; * ListNode(int x) : val(x), next(NULL) {} * }; */ ListNode* Solution::detectCycle(ListNode* A) { if(!A->next)return NULL; ListNode *tortoise=A; ListNode *hare=A; //check if there is a cycle while(hare){ if(hare->next and hare->next->next) hare=hare->next->next; else return NULL; //no cycle tortoise=tortoise->next; if(hare==tortoise)break; //cycle exists } ListNode* tortoise2 = A; while(tortoise2 != tortoise){ tortoise2 = tortoise2->next; tortoise = tortoise->next; } return tortoise; } |
Here is a golang implmentation if you are interested.
Other Uses of Floyd’s Cycle Finding Algorithm
Besides detecting cycles in a linked list, this algorithm can also be used in some other cases. For example, it can be used to identify cycles in any mathematical functions or pseudo-random number generator.
That’s it, now you know how cycle finding algorithm works. If you want to test yourself whether you are clear about this algorithm or not, you can try to solve this: uva 350 pseudo-random numbers.
If you want to read the same article in Bengali, click here.